PhD: Starving random walks First part: We develop a framework to determine the complete statistical behavior of a fundamental quantity in the theory of random walks, namely, the probability that n1, n2, n3, . . . distinct sites are visited at times t1, t2, t3, ... . From this multiple-time distribution, we show that the visitation statistics of 1d random walks are temporally correlated and we quantify the non-Markovian nature of the process. We exploit these ideas to derive unexpected results for the two-time trapping problem and also to determine the visitation statistics of two important stochastic processes, the run-and-tumble particle and the biased random walk (Arxiv link, published in Physical Review E ).
Exploration process of a one dimensional line by a random walker.
Second part: In this work, we introduce a fundamental quantity, the elapsed time τn between visits to the nth and the (n+1)st distinct sites, from which the full dynamics about the visitation statistics can be obtained. Despite the geometrical complexity of the territory explored by a random walk (typically aspherical, as well as containing holes and islands at all scales), we find that the distribution of the τn can be accounted for by simple analytical expressions. Processes as varied as regular diffusion, anomalous diffusion, and diffusion in disordered media and fractals, fall into the same universality classes for the temporal history of distinct sites visited. We confirm our theoretical predictions by Monte Carlo and exact enumeration methods. We also determine additional basic exploration observables, such as the perimeter of the visited domain or the number of islands of unvisited sites enclosed within this domain, thereby illustrating the generality of our approach. Because of their fundamental character and their universality, these inter-visit times represent a promising tool to unravel many more aspects of the exploration dynamics of random walks (Arxiv link, published in Nature Communications).
On the left, territory visited by the random walker in 2d: how long before finding food/a new site? On the right, representation of different exploration processes.
Third part: We introduce range-controlled random walks with hopping rates depending on the range N, that is, the total number of previously visited sites. We analyze a one-parameter class of models with a hopping rate Na, and determine the large time behavior of the average range, as well as its complete distribution in two limit cases. We find that the behavior drastically changes depending on whether the exponent a is smaller, equal, or larger than the critical value, ad, depending only on the spatial dimension d. When a>ad, the forager covers the infinite lattice in a finite time. The critical exponent is a1=2 and ad=1 when d≥2. We also consider the case of two foragers who compete for food, with hopping rates depending on the number of sites each visited before the other. Surprising behaviors occur in one dimension where a single walker dominates and finds most of the sites when a>1, while for a smaller than 1, the walkers evenly explore the line. We compute the gain of efficiency in visiting sites by adding one walker. (Arxiv link).
Illustration of a walker slowing down by visiting new sites.
Fourth part: How long is needed for an observable to exceed its previous highest value and establish a new record? This time, known as the age of a record plays a crucial role in quantifying record statistics. Until now, general methods for determining record age statistics have been limited to observations of either independent random variables or successive positions of a Markovian (memoryless) random walk. Here we develop a theoretical framework to determine record age statistics in the presence of memory effects for continuous non-smooth processes that are asymptotically scale-invariant. Our theoretical predictions are confirmed by numerical simulations and experimental realisations of diverse representative non-Markovian random walk models and real time series with memory effects, in fields as diverse as genomics, climatology, hydrology, geology and computer science. Our results reveal the crucial role of the number of records already achieved in time series and change our view on analysing record statistics.
(Nature Communications).
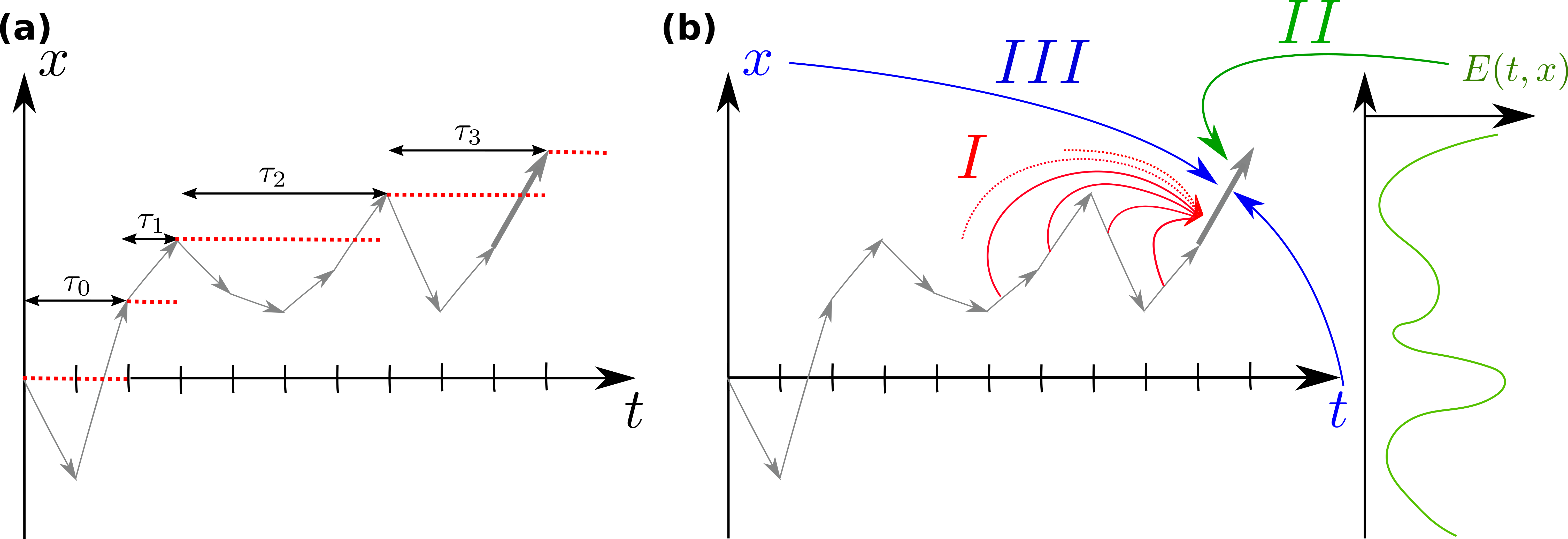Illustration of the record ages, considering the three rype of influences (I) memory of steps (II) interaction with an environment (III) space and time dependency.
Fifth part: Here, we solve the open d-dimensional starving random walk problem, in which each site of a lattice initially contains one food unit, consumed upon visit by the random walker, which can travel S steps without food before starving. Processes of diverse nature, including regular diffusion, anomalous diffusion, and diffusion in disordered media and fractals, share common properties within the same universality classes. To do so, we make a detour to extreme value statistics and determine the statistics of the maximum inter-visit time.
(PRL).
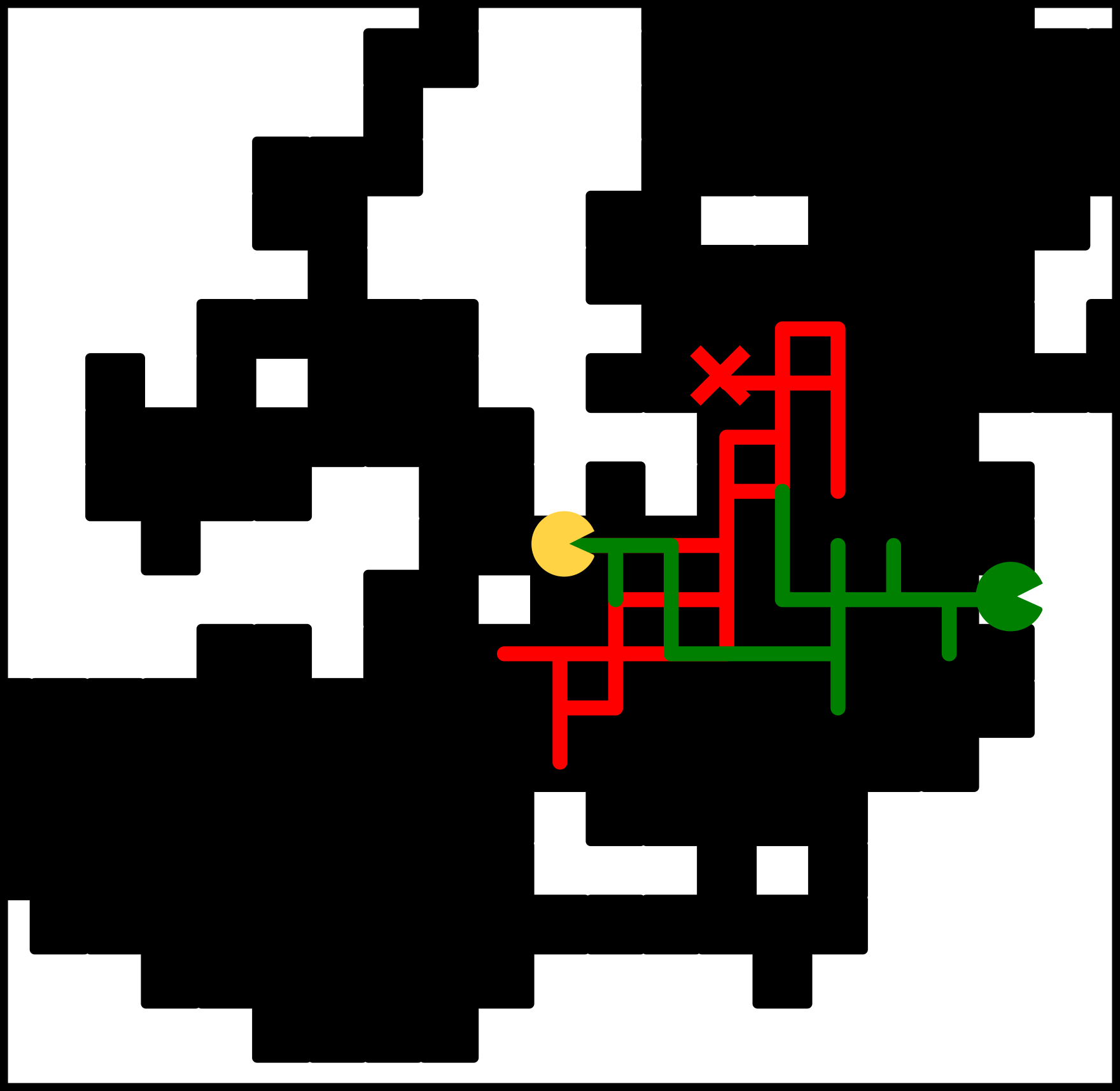Illustration of the starving RW process: the green trajectory finds a food unit before starving, the red one starves.
Sixth part: In this part, we develop a comprehensive framework for analyzing full record statistics, covering record counts M(t1),M(t2),…, and their corresponding attainment times TM(t1),TM(t2),…, as well as the intervals until the next record. From this multiple-time distribution, we derive general expressions for various observables related to record dynamics, including the conditional number of records given the number observed at a previous time and the conditional time required to reach the current record, given the occurrence time of the previous one. Our formalism is exemplified by a variety of stochastic processes, including biased nearest-neighbor random walks, asymmetric run-and-tumble dynamics, and random walks with stochastic resetting.
(Arxiv link).
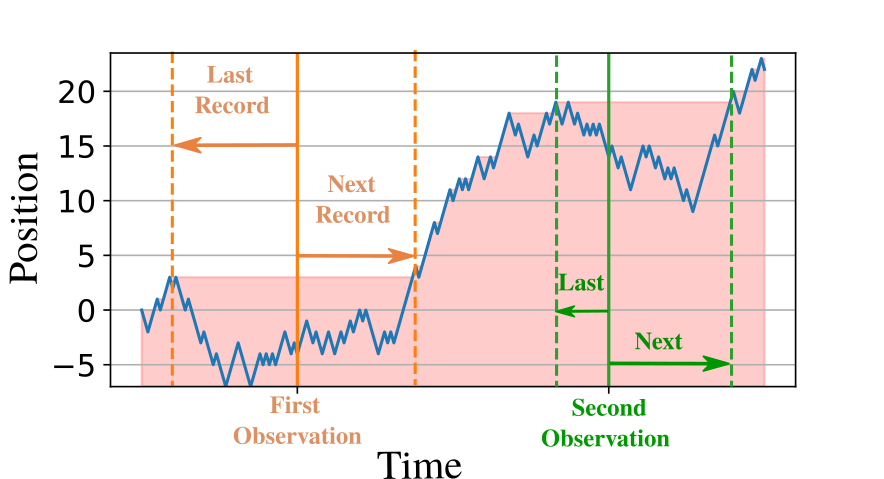The record process we characterize; the number record, the last and next records time of occurence.